Considere um circuito elétrico genérico como contendo \(n\) nós, circuito este planar e composto apenas de resistores, geradores de tensão e fontes de corrente.
Dessa forma, aplicando-se a Lei de Kirchhoff para as correntes, tal circuito pode ser descrito através de \(n\) equações nodais correspondentes, isto é,
\begin{equation} \left\lbrace \begin{array}{@{} l<{{}} @{} l @{}} \displaystyle\frac{v_{1}}{r_{11}} + \displaystyle\frac{v_{2}}{r_{12}} + \displaystyle\frac{v_{1}}{r_{13}} + \cdots + \displaystyle\frac{v_{n}}{r_{1n}} &= i_{1}\\ \displaystyle\frac{v_{1}}{r_{21}} + \displaystyle\frac{v_{2}}{r_{22}} + \displaystyle\frac{v_{1}}{r_{23}} + \cdots + \displaystyle\frac{v_{n}}{r_{2n}} &= i_{2}\\ \displaystyle\frac{v_{1}}{r_{31}} + \displaystyle\frac{v_{2}}{r_{32}} + \displaystyle\frac{v_{1}}{r_{33}} + \cdots + \displaystyle\frac{v_{n}}{r_{3n}} &= i_{3}\\ { }{}{ }{\vdots}&{}{}{}{\vdots}\\ \displaystyle\frac{v_{1}}{r_{n1}} + \displaystyle\frac{v_{2}}{r_{n2}} + \displaystyle\frac{v_{1}}{r_{n3}} + \cdots + \displaystyle\frac{v_{n}}{r_{nn}} &= i_{n}\\ \end{array} \right. \end{equation}
Observe que o sistema linear acima pode ser reescrito na forma de multiplicações entre matrizes, ou seja,
\begin{equation} \left( \begin{array}{ccccc} \Sigma_{11} & \Sigma_{12} & \Sigma_{13} & \cdots & \Sigma_{1n} \\ \Sigma_{21} & \Sigma_{22} & \Sigma_{33} & \cdots & \Sigma_{2n} \\ \Sigma_{31} & \Sigma_{32} & \Sigma_{33} & \cdots & \Sigma_{3n} \\ \vdots & \vdots & \vdots & \cdots & \vdots \\ \Sigma_{n1} & \Sigma_{n2} & \Sigma_{n3} & \cdots & \Sigma_{nn} \\ \end{array} \right) \times \left( \begin{array}{ccccc} v_{1}\\ v_{2}\\ v_{3}\\ \vdots\\ v_{n} \end{array} \right) =\left( \begin{array}{c} i_{1} \\ i_{2} \\ i_{3} \\ \vdots\\ i_{n} \end{array} \right) \label{equ:mainmat}\end{equation}
onde a letra grega sigma maíscula, \(\Sigma\), indica a condutância de um dado resistor e é dada como sendo o inverso da resistência desse dispositivo, ou seja, \(\Sigma_{ij} = 1/r_{ij}\).
Assim sendo, note que o determinante da matriz completa do sistema linear dado em (2) pode ser obtido através do Teorema de Laplace, isto é, através da k-ésima coluna tem-se:
\begin{equation} \begin{array}{rl} D &= \Sigma_{1k}(-1)^{1+k}D_{1k} + \Sigma_{2k}(-1)^{2+k}D_{1k} + \Sigma_{3k}(-1)^{3+k}D_{3k} + \cdots \\ {}&+ \cdots +(\Sigma_{kk} + \Sigma_{L})(-1)^{k+k}D_{kk} + \cdots + \Sigma_{nk}(-1)^{n+k}D_{nk} \end{array} \end{equation}
onde \(D_{ij}\) é o determinante da matriz resultante quando elimina-se da matriz completa a linha \(i\) e a coluna \(j\). Portanto, reordenando-se os termos e ponto em evidência a condutância \(\Sigma_{L}\), vem
\begin{equation} \begin{array}{rl} D &= [\Sigma_{1k}(-1)^{1+k}D_{1k} + \Sigma_{2k}(-1)^{2+k}D_{1k} + \Sigma_{3k}(-1)^{3+k}D_{3k} + \cdots \\ {}&+ \cdots +\Sigma_{kk}(-1)^{2k}D_{kk} + \cdots + \Sigma_{nk}(-1)^{n+k}D_{nk}] + [\Sigma_{L}(-1)^{2k}D_{kk}] \end{array} \end{equation}
Por fim, simplificando-se a expressão acima, vem
\begin{equation} D = D_{0} + [\Sigma_{L}D_{kk}] \label{equ:d}\end{equation}
Agora, aplicando-se a Regra de Cramer, vem
\begin{equation} v_{k} = \frac{det \begin{bmatrix} \Sigma_{11} & \Sigma_{12} & \cdots & \Sigma_{1(k-1)} & i_{1} & \Sigma_{1(k+1)} & \cdots & \Sigma_{1n} \\ \Sigma_{21} & \Sigma_{22} & \cdots & \Sigma_{2(k-1)} & i_{2} & \Sigma_{2(k+1)} & \cdots & \Sigma_{2n} \\ \Sigma_{31} & \Sigma_{32} & \cdots & \Sigma_{3(k-1)} & i_{3} & \Sigma_{3(k+1)} & \cdots & \Sigma_{3n} \\ \vdots & \vdots & {} & \vdots & \vdots & \vdots & {} & \vdots\\ \Sigma_{n1} & \Sigma_{n2} & \cdots & \Sigma_{n(k-1)} & i_{n} & \Sigma_{n(k+1)} & \cdots & \Sigma_{nn} \\ \end{bmatrix}}{D} \end{equation}
ou seja, através do teorema de Laplace aplicado à k-ésima coluna,
\begin{equation} v_{k} = \frac{i_{1}(-1)^{1+k}D_{ik} + i_{2}(-1)^{2+k}D_{2k} + \cdots + i_{n}(-1)^{n+k}D_{nk}}{D} \label{equ:vk}\end{equation}
Observe que pode-se reescrever a equação (\ref{equ:vk}) da seguinte forma
\begin{equation} v_{k} = \frac{i_{1}(-1)^{1+k}D_{ik} + i_{2}(-1)^{2+k}D_{2k} + \cdots + i_{n}(-1)^{n+k}D_{nk}}{D} \left(\frac{D_{0}}{D_{0}}\right) \end{equation}
isto é,
\begin{equation} v_{k} = \frac{i_{1}(-1)^{1+k}D_{ik} + i_{2}(-1)^{2+k}D_{2k} + \cdots + i_{n}(-1)^{n+k}D_{nk}}{D_{0}} \left(\frac{D_{0}}{D}\right) \label{equ:vk2}\end{equation}
Sabendo-se que:
\begin{equation} D_{0} = \Sigma_{1k}(-1)^{1+k}D_{1k} + \Sigma_{2k}(-1)^{2+k}D_{2k} + \cdots + \Sigma_{nk}(-1)^{n+k}D_{nk} \label{equ:do}\end{equation}
Portanto, substituindo-se as equações (\ref{equ:do}) e (\ref{equ:d}) em (\ref{equ:vk2}), obtém-se
\begin{equation} v_{k} = \frac{i_{1}(-1)^{1+k}D_{ik} + i_{2}(-1)^{2+k}D_{2k} + \cdots + i_{n}(-1)^{n+k}D_{nk}}{\Sigma_{1k}(-1)^{1+k}D_{1k} + \Sigma_{2k}(-1)^{2+k}D_{2k} + \cdots + \Sigma_{nk}(-1)^{n+k}D_{nk}} \left(\frac{D_{0}}{D}\right) \end{equation}
Note que o termo
\begin{equation} \frac{i_{1}(-1)^{1+k}D_{ik} + i_{2}(-1)^{2+k}D_{2k} + \cdots + i_{n}(-1)^{n+k}D_{nk}}{\Sigma_{1k}(-1)^{1+k}D_{1k} + \Sigma_{2k}(-1)^{2+k}D_{2k} + \cdots + \Sigma_{nk}(-1)^{n+k}D_{nk}} \end{equation}
corresponde à tensão de circuito aberto mensurada entre os terminais do resistor \(R_{L}\) (carga) ao removê-lo do circuito. Assim sendo, denominar-se-á tal grandeza por \(V_{th}\). Dessa forma,
\begin{equation} v_{k} = V_{th}\left(\frac{D_{0}}{D_{0} + [\Sigma_{L}D_{kk}]}\right) \end{equation}
Multiplicando-se tanto o numerador quanto o denominador da expressão acima por \(1/D_{0}\), vem
\begin{equation} v_{k} = V_{th}\left(\frac{1}{1 + \Sigma_{L}\displaystyle\left(\frac{D_{kk}}{D_{0}}\right)}\right) \end{equation}
Uma vez que a condutância da carga é dada por \(\Sigma_{L} = 1/R_{L}\), tem-se
\begin{equation} v_{k} = V_{th}\left(\frac{R_{L}}{R_{L} + \displaystyle\left(\frac{D_{kk}}{D_{0}}\right)}\right) \end{equation}
Observe que o termo \(\displaystyle\frac{D_{kk}}{D_{0}}\) possui unidade dada por \((1/\textrm{siemens}=\textrm{ohm})\). Portanto denomina-se arbitrariamente \(R_{th} = D_{kk}/D_{0}\). Dessa forma,
\begin{equation} v_{k} = V_{th}\left(\frac{R_{L}}{R_{L} + R_{th}}\right) \label{equ:div}\end{equation}
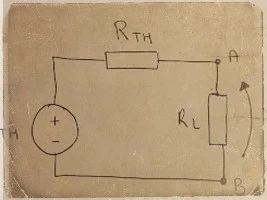
Observe que a expressão (\ref{equ:div}) acima representa o potencial elétrico sobre o resistor \(R_{L}\) segundo a equação do divisor de tensão aplicada ao circuito abaixo
Observe, inclusive, que o circuito genérico inicialmente idealizado é equivalente ao circuito de Thévenin descrito na figura (\ref{figthevenin}), onde denota-se por tensão equivalente de Thévenin, \(V_{th} = v_{oc}\), e por resistência equivalente de Thévenin, \(R_{th} = D_{kk}/D_{0}.\)
No entanto, o circuito equivalente de Thévenin foi calculado através de um dado k-ésimo nó. Assim sendo, deve-se, pois, demonstrar que o circuito equivalente encontrado é único, isto é, existe apenas um único circuito equivalente de Thévenin.
Referências
[Dorf e Svoboda] Dorf, R. C. e Svoboda, J. A. (2012). Introdução aos circuitos elétricos. LTC, Rio de Janeiro.
Comentários
Postar um comentário