Aplicação da Teoria Moderna de Portfólio de Markowitz com Python Utilizando Dados da Bolsa de Valores Brasileira (B3)

O presente artigo visa explorar a aplicação prática da Teoria Moderna de Portfólio (MPT) utilizando a linguagem de programação Python e dados provenientes da Bolsa de Valores Brasileira (B3). A análise foca em como esta teoria, apesar de suas limitações e críticas, pode ser eficazmente aplicada em um contexto contemporâneo e local. Embora a MPT dependa da variância como medida de risco, ela continua a ser uma ferramenta valiosa na gestão de investimentos, especialmente com o suporte de ferramentas modernas e acesso a dados robustos. A MPT permanece uma base sólida para a formulação de estratégias de investimento eficientes.

Harry Markowitz

Harry Markowitz, nascido em 24 de agosto de 1927, em Chicago, Illinois, emergiu como um dos economistas mais influentes do século XX. Filósofo por formação inicial, com grande interesse nas ideias de David Hume, Markowitz posteriormente dirigiu sua carreira para a economia, obtendo tanto o diploma de bacharel quanto o Ph.D. em Economia pela Universidade de Chicago. Sua trajetória foi marcadamente influenciada por sua participação na Cowles Commission for Research in Economics, um ambiente de excelência em pesquisa.

No início dos anos 1950, Markowitz ingressou na RAND Corporation, onde colaborou com George Dantzig, cuja expertise em técnicas de otimização foi fundamental para o desenvolvimento do algoritmo de linha crítica, destinado a identificar portfólios ótimos de média-variância. Esta colaboração culminou no desenvolvimento da "fronteira de Markowitz", uma ferramenta central na MPT. Em sua dissertação de 1954, Markowitz apresentou a teoria de portfólio, desafiando as convenções da época e lançando as bases para uma abordagem quantitativa na gestão de portfólios.

Teoria Moderna de Portfólio

A Teoria Moderna de Portfólio, introduzida por Markowitz em seu artigo seminal de 1952, "Portfolio Selection", revolucionou o campo de investimento ao oferecer um método sistemático para a construção de portfólios que maximizam o retorno esperado para um dado nível de risco, ou minimizam o risco para um retorno esperado. O framework da MPT introduziu conceitos-chave como diversificação e a fronteira eficiente, que se tornaram pilares das práticas financeiras modernas. Markowitz foi agraciado com o Prêmio Nobel de Economia em 1990, junto com Merton Miller e William Sharpe, por suas contribuições à economia financeira.

Diversificação e Gestão de Risco

A diversificação, um princípio fundamental da MPT, sustenta que a manutenção de uma gama diversificada de ativos pode reduzir o risco total do portfólio. Este conceito se baseia na premissa de que os preços dos ativos não se movem de forma perfeitamente correlacionada. A combinação de ativos com correlações não perfeitamente positivas permite a minimização do risco específico dos ativos. Por exemplo, a inclusão de títulos em um portfólio predominantemente composto por ações pode reduzir significativamente a volatilidade total do portfólio.

Fronteira Eficiente

A fronteira eficiente é um dos conceitos mais importantes da MPT, representando uma curva que ilustra os portfólios que oferecem o máximo retorno esperado para um determinado nível de risco. Portfólios localizados na fronteira eficiente são considerados ótimos, pois maximizam o retorno para seus níveis de risco. Em contraste, portfólios que ficam abaixo dessa fronteira são sub-ótimos, pois não compensam suficientemente o risco assumido. Por exemplo, entre dois portfólios com o mesmo retorno esperado, o portfólio com menor desvio padrão é preferível, pois apresenta menor risco.

Algumas Críticas

Apesar de sua robustez, a MPT enfrenta críticas, especialmente quanto ao uso da variância como medida de risco, que pode não refletir adequadamente a aversão ao risco de investidores, particularmente em cenários de queda de mercado. Além disso, a "diversificação ingênua" — a alocação equitativa de recursos entre diferentes ativos — pode, em alguns casos, superar a alocação otimizada sugerida pela MPT, dependendo das condições de mercado. Modelos alternativos, como o modelo Black–Litterman e a Teoria Pós-Moderna do Portfólio, foram desenvolvidos para abordar essas limitações, incorporando visões subjetivas e medidas de risco alternativas.

Aplicação com Dados da B3

Este estudo explora a aplicação prática dos conceitos da Teoria Moderna de Portfólio (MPT) utilizando dados reais da Bolsa de Valores Brasileira (B3). Focaremos nos efeitos do risco, da rentabilidade, da correlação e da diversificação de ativos sobre a possível rentabilidade de uma carteira de investimentos.

Preparando o Computador

Para realizar este estudo, é crucial ter acesso a um computador com Python e Jupyter Notebook instalados, que permitirão a execução dos códigos e a análise dos dados de forma interativa e eficiente. Alternativamente, o Google Colab oferece uma plataforma gratuita baseada na nuvem, ideal para executar códigos Python sem necessidade de instalações locais, facilitando a reprodução dos passos apresentados.

Independente da escolha, essas ferramentas possibilitarão uma exploração completa dos dados e dos resultados, oferecendo um ambiente adequado para o desenvolvimento de análises quantitativas.

Importando Bibliotecas Necessárias

A seguir, procederemos com a importação das bibliotecas fundamentais para nossa análise. Estas bibliotecas nos fornecerão as ferramentas necessárias para manipulação de dados, cálculos financeiros e visualização gráfica:

• Pandas: Essencial para manipulação e análise de dados, especialmente em formato tabular, como séries temporais de preços de ativos.
• NumPy: Utilizada para operações numéricas eficientes, incluindo cálculos de estatísticas descritivas e manipulação de arrays multidimensionais.
• Matplotlib: Biblioteca de visualização gráfica que permitirá a criação de gráficos para a análise visual dos dados e dos resultados.
• yfinance: Ferramenta específica para a obtenção de dados históricos de preços de ativos financeiros, facilitando o acesso aos dados necessários para o estudo.

Essas bibliotecas são fundamentais para realizar uma análise quantitativa robusta, permitindo a construção de gráficos detalhados e uma exploração interativa dos dados. Abaixo, demonstramos como importar essas bibliotecas e suas funções principais:

# Instalação dos pacotes
from datetime import datetime  # Função datetime do módulo datetime
from pathlib import Path       # Classe Path do módulo pathlib
from IPython import display    # Módulo display do pacote IPython, 
                               # usado para limpar a saída do notebook

# Função para limpar a saída do notebook
def clear():
    display.clear_output(wait=True)
    display.clear_output()

# Leitura e escrita de arquivos CSV, manipulação de DataFrames.
try:    
    import pandas as pd  
except:
    !pip install pandas  
    import pandas as pd  
    clear()

# Facilita a extração de dados financeiros e econômicos de fontes online para 
# análise com pandas.
try:
    from pandas_datareader import data as web  
except:
    !pip install --upgrade pandas_datareader   
    from pandas_datareader import data as web  
    clear()

# Download de dados históricos de ações e índices, análise de séries temporais 
# financeiras
try:
  import fix_yahoo_finance as yf
except:
  !pip install fix_yahoo_finance --upgrade --no-cache-dir
  import fix_yahoo_finance as yf
  clear()

# Download de dados históricos de ações e índices, análise de séries temporais 
# financeiras.
# Bug: Não funciona mais desde a última atualização, usar fix_yahoo_finance.
#
#try:
#    import yfinance as yf  
#except:
#    !pip install yfinance  
#    import yfinance as yf  
#    clear()
#finally:
#    yf.pdr_override()  # Configura o pandas_datareader para usar o yfinance

# Criação de gráficos de linhas, barras, dispersão e histogramas.
try:
    import matplotlib.pyplot as plt  
except:
    !pip install matplotlib          
    import matplotlib.pyplot as plt  
    clear()

# Otimização de portfólio, cálculo de medidas de risco, análise de performance.
try:
    import riskfolio as rp      
except:
    !pip install riskfolio-lib  
    import riskfolio as rp      
    clear()

# Operações matemáticas e estatísticas em arrays, álgebra linear, 
# manipulação de grandes conjuntos de dados numéricos.    
try:
    import numpy as np  
except:
    !pip install numpy  
    import numpy as np  
    clear()

# Previsão de vendas, previsão de demanda, análise de tendências e sazonalidades 
# em dados temporais.
try:
    from prophet import Prophet  
except:
    !pip install prophet  
    from prophet import Prophet   
    clear()

Seleção do Período de Análise para Dados Históricos

Definir um período específico para a análise dos dados históricos é fundamental para garantir uma compreensão precisa e abrangente do desempenho dos ativos. Um intervalo de aproximadamente cinco anos é recomendado, pois permite capturar tendências de longo prazo, ciclos de mercado e variações significativas nos preços dos ativos. Essa escolha temporal é essencial para uma análise robusta, pois oferece uma base sólida para identificar padrões consistentes e comportamentos subjacentes nos dados.

E, ao determinar o período de análise, é crucial levar em conta eventos econômicos significativos, mudanças regulatórias, e outros fatores externos que possam ter impactado o mercado de maneira relevante. Por exemplo, crises econômicas, mudanças nas políticas monetárias ou fiscais, e outros eventos macroeconômicos podem influenciar de forma substancial os preços dos ativos.

# Período para análise dos dados históricos
data_inicial    = datetime.strptime('2018-08-01', '%Y-%m-%d') # data inicial para começar análise
data_final      = datetime.strptime('2024-08-01', '%Y-%m-%d') # data final para finalizar análise

Com o período de análise estabelecido, podemos proceder à coleta dos dados históricos de preços dos ativos e à subsequente análise. Em nosso exemplo, a seleção de um intervalo de cinco anos permitirá avaliar a performance dos ativos em diferentes condições de mercado, proporcionando uma visão clara sobre como eles respondem a variações econômicas e tendências de mercado.

Seleção dos Ativos para Análise (IBrX 50)

Após a definição do período de análise para os dados históricos, a próxima etapa essencial é a seleção dos ativos a serem estudados. Para este estudo, optamos por focar em ativos que representem uma ampla gama de empresas brasileiras listadas na Bolsa de Valores B3. Para isso, utilizaremos o índice IBrX 50, que serve como um indicador representativo do desempenho médio dos 50 ativos mais negociados e de maior relevância no mercado de ações brasileiro.

O índice IBrX 50 é composto por ativos que atendem a critérios rigorosos, garantindo uma representação fiel do mercado. Os principais critérios para inclusão são:

1. Índice de negociabilidade (IN): Os ativos devem estar entre os 50 primeiros em ordem decrescente de IN, considerando um buffer de 90%. Isso assegura a seleção de ativos com alta liquidez, refletindo uma negociação consistente e relevante.

2. Presença em pregão: Os ativos selecionados devem ter uma presença mínima de 95% nos pregões. Essa alta frequência de negociação é fundamental para garantir que os ativos sejam representativos e relevantes no mercado.

3. Exclusão de penny stocks: Para manter a qualidade e representatividade do índice, ativos classificados como penny stocks (ações de baixo valor) são excluídos. Essa exclusão evita a inclusão de ativos altamente especulativos e de baixa capitalização, que poderiam distorcer a análise.

Para a realização da análise, vamos extrair uma amostra dos ativos do índice IBrX 50. Essa seleção permitirá estudar o comportamento de uma parte representativa do mercado, facilitando a compreensão das dinâmicas e tendências observadas. A escolha do IBrX 50 como referência oferece uma visão abrangente do mercado, capturando a performance de empresas de diversos setores econômicos. 

O código a seguir ilustra o processo de extração de dados para uma seleção de ativos do IBrX 50, utilizando ferramentas de acesso a dados financeiros:

# Obtém ativos do índice IBrX 50 da B3
import requests
import ipywidgets as widgets
from IPython.display import display

url = "https://sistemaswebb3-listados.b3.com.br/indexProxy/indexCall/GetPortfolioDay/eyJsYW5ndWFnZSI6InB0LWJyIiwicGFnZU51bWJlciI6MSwicGFnZVNpemUiOjYwLCJpbmRleCI6IklCWEwiLCJzZWdtZW50IjoiMiJ9?pageSize=60"

headers = {
    "Accept": "application/json, text/plain, */*",
    "Accept-Encoding": "gzip, deflate, br, zstd",
    "Accept-Language": "pt-BR,pt;q=0.9,en-US;q=0.8,en;q=0.7,fr;q=0.6,en-GB;q=0.5",
    "Connection": "keep-alive",
    "Host": "sistemaswebb3-listados.b3.com.br",
    "Referer": "https://sistemaswebb3-listados.b3.com.br/",
    "Sec-Ch-Ua": "\"Not A(Brand\";v=\"99\", \"Chromium\";v=\"121\", \"Google Chrome\";v=\"121\"",
    "Sec-Ch-Ua-Mobile": "?1",
    "Sec-Ch-Ua-Platform": "\"Android\"",
    "Sec-Fetch-Dest": "empty",
    "Sec-Fetch-Mode": "cors",
    "Sec-Fetch-Site": "same-origin",
    "User-Agent": "Mozilla/5.0 (Linux; Android 6.0; Nexus 5 Build/MRA58N) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/121.0.0.0 Mobile Safari/537.36",
}

# Fazendo a requisição
response = requests.get(url, headers=headers, verify = False)

data = response.json()

# Agrupar os códigos (tickers) por segmento
tickers_por_segmento = {}
for result in data['results']:
    segmento = result['segment']
    ticker = result['cod']
    if segmento not in tickers_por_segmento:
        tickers_por_segmento[segmento] = []
    tickers_por_segmento[segmento].append(ticker)

# Criar checkboxes para cada segmento
checkboxes = {}
for segmento, tickers in tickers_por_segmento.items():
    checkboxes[segmento] = widgets.Checkbox(description=f"{tickers} - {segmento}", layout=widgets.Layout(width='auto'))

# Checkbox "Selecionar todos"
checkbox_select_all = widgets.Checkbox(description="Selecionar todos", layout=widgets.Layout(width='auto'))

# Exibir checkboxes
checkboxes_widgets = [checkboxes[segmento] for segmento in checkboxes.keys()]
checkboxes_box = widgets.VBox([checkbox_select_all] + checkboxes_widgets)
display(checkboxes_box)

# Função para selecionar ou deselecionar todos os checkboxes
def select_all_checkboxes(change):
    for checkbox in checkboxes.values():
        checkbox.value = change.new

# Adicionar o manipulador de eventos ao checkbox "Selecionar todos"
checkbox_select_all.observe(select_all_checkboxes, 'value')

Resultados da Seleção de Ativos

Após a execução do código de coleta de dados, obtivemos a lista de ativos selecionados do índice IBrX 50. A seguir, apresentamos os ativos que foram incluídos no estudo, representando uma amostra diversificada e representativa do mercado de ações brasileiro. Todos os ativos listados foram escolhidos com base nos critérios previamente definidos e foram incluídos na análise para fornecer uma visão abrangente das dinâmicas e tendências do mercado.

Flexibilidade na Seleção de Ativos

A metodologia de seleção de ativos não se limita apenas ao índice IBrX 50. O código pode ser facilmente adaptado para incluir uma variedade de índices que representam setores ou características específicas do mercado. Essa flexibilidade é essencial para a condução de análises mais direcionadas e personalizadas, permitindo uma exploração detalhada de diferentes segmentos do mercado financeiro. Seguem alguns exemplos de índices alternativos.

1. Índice de agronegócio: Focado em empresas do setor agropecuário, este índice inclui ativos de companhias envolvidas em atividades agrícolas, pecuárias e de produtos relacionados, oferecendo uma visão especializada sobre o desempenho desse setor vital para a economia brasileira.

2. Índice de BDRs não patrocinados-global: Este índice é composto por Brazilian Depositary Receipts (BDRs) não patrocinados, que representam ações de empresas estrangeiras. Ele permite uma análise do desempenho de ativos internacionais negociados na B3, expandindo o escopo do estudo para além das fronteiras nacionais.

3. Índice de consumo: Engloba empresas do setor de consumo, incluindo tanto bens de consumo duráveis quanto não duráveis. Este índice é útil para estudar a sensibilidade desses ativos a fatores macroeconômicos e mudanças nos padrões de consumo.

4. Índice smart dividendos: Focado em empresas que oferecem dividendos consistentes e atrativos, este índice é ideal para investidores interessados em renda passiva. A análise de empresas com forte histórico de pagamento de dividendos pode fornecer insights sobre estratégias de investimento baseadas em dividendos.

5. Índice do setor elétrico: Composto por empresas do setor de energia elétrica, este índice permite uma análise focada em um setor essencial e regulamentado, que possui características distintas em termos de risco e retorno.

A flexibilidade na seleção de índices permite que o estudo seja ajustado para atender a objetivos de pesquisa específicos. Por exemplo, um investidor interessado em explorar o desempenho do agronegócio pode adaptar o código para focar exclusivamente no Índice de Agronegócio. Da mesma forma, a inclusão de BDRs possibilita a análise de ativos internacionais, proporcionando uma perspectiva global.

Essa capacidade de personalização é valiosa tanto para acadêmicos quanto para profissionais de investimento, pois permite a adaptação das análises a diferentes cenários e necessidades. A escolha dos índices e dos ativos a serem analisados pode ser orientada por diversas estratégias de investimento, como foco em crescimento, rendimento, ou diversificação internacional.

No caso, para ajustar o código para outros índices, basta modificar a lista de tickers de acordo com os ativos pertencentes ao índice de interesse. A coleta de dados e a análise subsequente podem então ser realizadas seguindo o mesmo procedimento descrito anteriormente, garantindo uma análise robusta e direcionada conforme o objetivo específico do estudo.

Definindo os Ativos

Com os ativos devidamente selecionados, o próximo passo é coletar informações financeiras históricas para cada um dos tickers. Essa etapa é fundamental para realizar análises detalhadas, pois os dados históricos nos fornecem insights sobre o desempenho passado dos ativos, incluindo preços, volumes de negociação, dividendos, e outros indicadores financeiros relevantes.

# Função para retornar os tickers selecionados com base nas checkboxes
def get_selected_tickers(checkboxes_dict, tickers_dict):
    # lista para armazenar tickers selecionados
    selected_tickers = []
    for segmento, checkbox in checkboxes_dict.items():
        try:
            if checkbox.value:
                try:
                  selected_tickers.extend(tickers_dict[segmento])
                except NameError:
                  pass 
        except NameError:
            pass 
    return selected_tickers

# Definindo os dicionários de checkboxes e tickers
checkboxes_dict = {
    'IBrX 50': globals().get('checkboxes', {}),
}

tickers_dict = {
    'IBrX 50': globals().get('tickers_por_segmento', {}),
}

# Obtém os tickers selecionados
tickers_yahoo = []
for segmento, checkboxes_dict in checkboxes_dict.items():
    tickers_yahoo.extend(get_selected_tickers(checkboxes_dict, tickers_dict[segmento]))

# Adicionando .SA aos tickers selecionados
tickers_yahoo = [ticker + '.SA' for ticker in tickers_yahoo]

# Remove duplicações
tickers_yahoo = list(set(tickers_yahoo))

print("Tickers selecionados:", tickers_yahoo)

Após a execução da célula anterior, os ativos correspondentes foram selecionados com sucesso. Abaixo estão os tickers dos ativos escolhidos para o estudo:

Tickers selecionados: ['MRVE3.SA', 'LREN3.SA', 'ASAI3.SA', 'MGLU3.SA', 'SUZB3.SA', 'EGIE3.SA', 'AZUL4.SA', 'ABEV3.SA', 'BBSE3.SA', 'SANB11.SA', 'CYRE3.SA', 'PETR4.SA', 'BPAC11.SA', 'B3SA3.SA', 'SBSP3.SA', 'USIM5.SA', 'EMBR3.SA', 'UGPA3.SA', 'ITSA4.SA', 'CSNA3.SA', 'RRRP3.SA', 'CMIG4.SA', 'TIMS3.SA', 'KLBN11.SA', 'ELET3.SA', 'CPLE6.SA', 'RENT3.SA', 'ALOS3.SA', 'CIEL3.SA', 'CPFE3.SA', 'JBSS3.SA', 'HAPV3.SA', 'EQTL3.SA', 'NTCO3.SA', 'BBAS3.SA', 'GGBR4.SA', 'MULT3.SA', 'BRFS3.SA', 'ITUB4.SA', 'CSAN3.SA', 'VBBR3.SA', 'BBDC4.SA', 'HYPE3.SA', 'PRIO3.SA', 'WEGE3.SA', 'RADL3.SA', 'PETR3.SA', 'RDOR3.SA', 'VALE3.SA', 'TOTS3.SA', 'RAIL3.SA', 'AZZA3.SA']

Esses ativos foram selecionados de acordo com os critérios estabelecidos anteriormente, garantindo uma análise abrangente e diversificada. Com essa seleção, podemos proceder para a coleta e análise dos dados financeiros históricos, proporcionando uma base sólida para as próximas etapas da pesquisa.

Obtendo os Dados dos Tickers

Com a lista de tickers selecionados, o próximo passo é adquirir os dados financeiros históricos para cada um desses ativos. Este processo envolve a coleta de informações como preços de abertura e fechamento, máximas e mínimas diárias, volume de negociação e outros indicadores relevantes.

# Obtendo os dados dos tickers
dados_tickers = yf.download(tickers_yahoo, start=data_inicial, end=data_final)

# Lidar com dados ausentes: Preencher valores ausentes com a média da coluna
dados_tickers.fillna(dados_tickers.mean(), inplace=True)

# Verificar tipos de dados e converter se necessário (por exemplo, datas para datetime)
dados_tickers.index = pd.to_datetime(dados_tickers.index)

# Exibindo os primeiros registros dos dados
print(dados_tickers.head())

Aplicação do Método de Markowitz

Com os dados históricos dos preços das ações em mãos, estamos prontos para aplicar o Método de Markowitz para otimizar nosso portfólio. Este método é fundamental para a construção de portfólios eficientes, buscando maximizar o retorno esperado para um nível de risco específico ou minimizar o risco para um nível de retorno esperado.

4.1 Criando o DataFrame de Variação

O primeiro passo é criar um DataFrame que contenha as variações dos preços de fechamento ajustados das ações. Esse DataFrame nos permitirá calcular retornos diários e analisar a volatilidade dos ativos, o que é essencial para a aplicação do Método de Markowitz.

Para isso, seguiremos os seguintes passos:

1. Coletar os preços de fechamento ajustados: Obteremos os preços de fechamento ajustados para cada ação.
2. Calcular as variações: Calcularemos a variação percentual diária dos preços de fechamento ajustados.
3. Criar o DataFrame: Organizar essas variações em um DataFrame para facilitar a análise e o cálculo dos parâmetros necessários para a otimização do portfólio.

Este DataFrame será a base para a análise de risco e retorno do portfólio, permitindo a aplicação do Método de Markowitz de maneira eficaz.

# Calculando a variação dos preços de fechamento ajustados
variacao_df = dados_tickers['Adj Close'].pct_change().dropna()

# Exibindo as primeiras linhas do DataFrame de variação
print(variacao_df.head())

Instanciando a Classe "Portfólio"

Para aplicar o Método de Markowitz, o primeiro passo é instanciar a classe Portfolio. Esta classe é essencial para o cálculo dos retornos esperados e da matriz de covariância dos ativos com base nos dados históricos que coletamos.

A classe Portfolio nos permitirá:

1. Calcular retornos esperados: Determinar o retorno médio esperado de cada ativo no portfólio com base em seus preços históricos.
2. Construir a matriz de covariância: Calcular a matriz de covariância que descreve como os retornos dos ativos variam em relação uns aos outros, o que é fundamental para avaliar o risco do portfólio.
3. Otimizar o portfólio: Utilizar os retornos esperados e a matriz de covariância para encontrar a combinação ótima de ativos que maximiza o retorno para um dado nível de risco ou minimiza o risco para um nível de retorno esperado.

Instanciando a classe Portfolio, estaremos preparados para prosseguir com a aplicação do Método de Markowitz e realizar a otimização do nosso portfólio de investimentos.

# Instanciando a classe Portfolio com os retornos históricos
portfolio = rp.Portfolio(returns = variacao_df)

Definindo Métodos para Cálculo de Retornos Históricos

Para calcular os retornos esperados e a matriz de covariância, definiremos os métodos a serem utilizados. Esses métodos são fundamentais para a análise e otimização do portfólio, proporcionando a base necessária para o Método de Markowitz.

# define o método de retornos histórico para calcular o retorno esperado
metodo_mu = 'hist'

# define o método de retornos histórico para calcular a matriz de covariância
metodo_cov = 'hist'

Onde,

1. Método de retornos esperados (metodo_mu): o método 'hist' indica que usaremos o cálculo baseado em dados históricos para estimar o retorno esperado de cada ativo. Isso envolve calcular a média dos retornos diários históricos, que fornecerá uma estimativa do retorno esperado para cada ativo no portfólio.

2. Método de matriz de covariância (metodo_cov): similarmente, o método 'hist' para a matriz de covariância significa que utilizaremos a covariância baseada em dados históricos para avaliar como os retornos dos ativos variam em relação uns aos outros. Isso é feito calculando a matriz de covariância a partir das variações diárias dos preços de fechamento ajustados.

Com esses métodos definidos, estamos preparados para calcular os retornos esperados e a matriz de covariância, permitindo uma análise completa e a otimização do nosso portfólio de investimentos.

Calculando o Método de Otimização

Após definir os métodos para calcular os retornos esperados e a matriz de covariância, o próximo passo é aplicar esses métodos para otimizar o portfólio. Este processo envolve o cálculo dos atributos estatísticos dos ativos, que são essenciais para a análise de risco e retorno.

base necessária para o Método de Markowitz.

# Calculando os atributos estatísticos dos ativos
portfolio.assets_stats(method_mu=metodo_mu, method_cov=metodo_cov)

Onde,

1. Método de Cálculo (assets_stats):

   • Descrição: O método assets_stats é utilizado para calcular os atributos estatísticos dos ativos no portfólio. Ele utiliza os métodos definidos anteriormente (metodo_mu para retornos esperados e metodo_cov para a matriz de covariância) para gerar estatísticas essenciais.
   • Parâmetros:
     • method_mu: Especifica o método para calcular os retornos esperados, definido como 'hist' para basear-se em dados históricos.
     • method_cov: Especifica o método para calcular a matriz de covariância, também definido como 'hist'.
     • d (opcional): Este parâmetro é usado para suavizar a matriz de covariância com um fator de decaimento exponencial. Se não for fornecido, o valor padrão será usado.

Observe que o cálculo desses atributos estatísticos permitirá avaliar o desempenho esperado de cada ativo e entender como eles interagem no portfólio. Esses dados são fundamentais para otimizar a alocação dos ativos e construir um portfólio que maximize o retorno esperado para um nível de risco específico ou minimize o risco para um nível de retorno esperado.

Após calcular os atributos estatísticos, estaremos prontos para prosseguir com a otimização do portfólio, utilizando esses dados para encontrar a melhor combinação de ativos.

Parâmetros para o Modelo Clássico de Markowitz

Agora, vamos configurar os parâmetros para o Modelo Clássico de Markowitz (MCM).

model = 'Classic' # Modelo clássico de Markowitz
rm    = 'MV'      # Medida de risco: mean-variance
obj   = 'Sharpe'  # Função objetivo: Maximizar Shape

Para os parâmetros model, rm e obj, existem várias opções disponíveis. Aqui estão algumas alternativas:

Para o parâmetro model

• Classic: Modelo clássico de Markowitz. O modelo clássico de Markowitz é uma abordagem amplamente utilizada para a otimização de carteiras de investimento. Ele busca a alocação de ativos que maximize o retorno esperado para um determinado nível de risco, levando em consideração a relação entre os diferentes ativos.
• FM: Filtro de Medvedev (Medvedev Filtering). O Filtro de Medvedev é uma técnica que suaviza os retornos de ativos individuais antes de realizar a otimização da carteira. Isso ajuda a reduzir a volatilidade dos retornos e pode levar a uma alocação mais estável de ativos.
• RP: Paridade de Risco (Risk Parity). A Paridade de Risco é uma abordagem que busca equilibrar o risco entre os diferentes ativos em uma carteira, atribuindo pesos de forma que a contribuição de cada ativo para o risco total da carteira seja igual.
• ERC: Equal Risk Contribution. O Equal Risk Contribution é um método que busca distribuir o risco de forma igual entre os ativos da carteira, garantindo que cada ativo contribua de maneira equitativa para o risco total da carteira.
• MinRisk: Minimizar o risco. Este método visa minimizar o risco total da carteira, levando em consideração as correlações entre os diferentes ativos e buscando uma alocação que reduza a volatilidade da carteira.
• CDaR: Conditional Drawdown at Risk. O Conditional Drawdown at Risk é uma medida de risco que se concentra em períodos de drawdown (redução no valor da carteira). Este método visa maximizar o retorno esperado da carteira enquanto mantém o drawdown abaixo de um certo limite.
• EDaR: Entropic Drawdown at Risk. O Entropic Drawdown at Risk é uma abordagem que utiliza a teoria da informação para quantificar o risco de drawdown da carteira. Ele leva em consideração a distribuição probabilística dos retornos para estimar o risco de drawdown.
• ERC_RMAD: Equal Risk Contribution - Risk Measure Absolute Deviation um método de alocação de ativos que visa garantir uma contribuição igual de risco de cada ativo na carteira. Ele utiliza o desvio médio absoluto (MAD) como medida de risco e otimiza a alocação para que cada ativo contribua igualmente para o risco total da carteira, em termos absolutos. Isso promove uma distribuição mais equilibrada do risco entre os ativos, reduzindo a concentração de risco em determinados ativos e melhorando a diversificação da carteira.

Para o parâmetro rm (Medida de Risco)

• MV: Desvio padrão (Mean-Variance). O desvio padrão é uma medida de dispersão que indica o quanto os retornos de uma carteira de investimentos variam em relação à sua média. Quanto maior o desvio padrão, maior a volatilidade e, portanto, maior o risco percebido da carteira.
• MAD: Desvio médio absoluto. O desvio médio absoluto é uma medida de risco que calcula a média das diferenças absolutas entre os retornos da carteira e sua média. Ele é menos sensível a outliers do que o desvio padrão e fornece uma medida mais robusta da dispersão dos retornos.
• MSV: Desvio Semi-Padrão. O desvio semi-padrão é uma medida de risco que se concentra apenas nos retornos negativos da carteira, ignorando os retornos positivos. Isso faz com que seja uma medida mais conservadora, focada apenas no risco de queda.
• FLPM: Ômega Ratio. O Ômega Ratio é uma medida de risco que compara o retorno médio da carteira com uma medida de risco de cauda, representando a proporção de retornos negativos em relação ao retorno médio.
• SLPM: Sortino Ratio. O Sortino Ratio é uma medida de risco que considera apenas o risco de queda da carteira, utilizando apenas os retornos negativos para calcular o risco. Isso o torna uma medida mais precisa de risco em comparação com o Ômega Ratio.
• CVaR: Valor Condicional em Risco. O Valor Condicional em Risco é uma medida de risco que quantifica a perda média esperada da carteira além de um certo nível de confiança, geralmente associado a situações extremas de mercado.
• EVaR: Entropic Value at Risk. O Valor Entrópico em Risco é uma medida de risco que utiliza a entropia como medida de incerteza na distribuição de retornos. Ele fornece uma estimativa da perda potencial da carteira considerando a incerteza associada aos diferentes cenários de retorno.
• WR: Valor Entrópico em Risco. O Valor Entrópico em Risco é útil para investidores que desejam entender a incerteza associada aos retornos de um ativo ou de uma carteira. Ele fornece uma medida de risco que leva em consideração a distribuição de probabilidades dos retornos, oferecendo uma perspectiva mais completa do risco envolvido em uma estratégia de investimento.
• MDD: Calmar Ratio. A Mean-Downside Deviation é uma medida de risco que se concentra nos retornos abaixo de um determinado limiar de tolerância (geralmente zero ou o retorno desejado). Essa medida penaliza mais os retornos negativos, refletindo uma aversão maior ao risco de queda.
• ADD: Average Drawdown of uncompounded cumulative returns. A Average Drawdown é uma medida de risco que calcula a média dos drawdowns (reduções no valor da carteira em relação ao seu pico anterior) ao longo de um determinado período. Quanto maior a média dos drawdowns, maior o risco percebido da carteira.
• CDaR: Conditional Drawdown at Risk of uncompounded cumulative returns. O Conditional Drawdown at Risk é valioso para investidores que estão preocupados com a possibilidade de perdas significativas em suas carteiras durante períodos específicos. Ele ajuda os investidores a entenderem o máximo esperado de perda durante um período de tempo específico, com base em um nível de confiança definido. Isso permite uma gestão mais precisa do risco e uma melhor preparação para cenários adversos.
• EDaR: Entropic Drawdown at Risk of uncompounded cumulative returns. O Entropic Drawdown at Risk é útil para investidores que desejam uma medida de risco que leve em conta a incerteza associada aos drawdowns (reduções) da carteira. Ao considerar a distribuição de probabilidades dos drawdowns e a entropia dessa distribuição, o EDaR oferece uma visão mais abrangente do risco de reduções significativas no valor da carteira. Isso pode ajudar os investidores a tomar decisões mais informadas sobre alocação de ativos e gestão de risco.
• UCI: Ulcer Index of uncompounded cumulative returns. O Índice de Úlcera é uma medida de risco que quantifica a magnitude e a duração das reduções no valor da carteira ao longo do tempo. Ele é calculado com base nos drawdowns da carteira e fornece uma medida composta do risco de queda.

Para o parâmetro obj (Função objetivo)

• Sharpe: Maximizar o Índice de Sharpe. Esta função objetivo é usada para maximizar o Índice de Sharpe de uma carteira. O Índice de Sharpe é uma medida de desempenho ajustada ao risco que avalia o retorno de um investimento em relação ao seu risco. Maximizar o Índice de Sharpe resulta em uma carteira que oferece o melhor equilíbrio entre retorno e risco.
• RP: Maximizar a Paridade de Risco. Esta função objetivo é usada para maximizar a Paridade de Risco de uma carteira. A Paridade de Risco é uma abordagem que busca equilibrar o risco entre os diferentes ativos em uma carteira, garantindo que cada ativo contribua igualmente para o risco total da carteira. Maximizar a Paridade de Risco resulta em uma carteira onde o risco é distribuído de forma equitativa entre os ativos.
• MinRisk: Minimizar o risco. Esta função objetivo é usada para minimizar o risco total de uma carteira. Ela busca criar uma carteira que ofereça o menor nível de risco possível, independentemente do retorno. Isso pode ser adequado para investidores que têm uma aversão ao risco e priorizam a preservação do capital sobre o potencial de retorno.
• CDaR: Maximizar o Conditional Drawdown at Risk. Esta função objetivo é usada para maximizar o Conditional Drawdown at Risk de uma carteira. O Conditional Drawdown at Risk é uma medida de risco que avalia a magnitude máxima esperada de uma redução no valor da carteira durante um período de tempo específico, com base em um nível de confiança definido. Maximizar o Conditional Drawdown at Risk resulta em uma carteira que está preparada para enfrentar perdas potenciais durante períodos de tempo especificados.
• EDaR: Maximizar o Entropic Drawdown at Risk. Esta função objetivo é usada para maximizar o Entropic Drawdown at Risk de uma carteira. O Entropic Drawdown at Risk é uma medida de risco que leva em consideração a incerteza associada aos drawdowns (reduções) na carteira. Ao maximizar o Entropic Drawdown at Risk, a carteira é projetada para lidar efetivamente com a incerteza e a variabilidade nos drawdowns, proporcionando uma proteção adicional contra perdas significativas.

Essas são apenas algumas opções disponíveis. Você pode escolher a que melhor se adapta às suas necessidades e objetivos de investimento.

Criando a Carteira de Investimentos

Com os atributos estatísticos dos ativos calculados e o método de otimização definido, o próximo passo é criar a carteira de investimentos otimizada. Este processo envolve a aplicação dos modelos e critérios estabelecidos para determinar a melhor alocação de ativos.

# Criando a carteira de investimentos
carteira = portfolio.optimization(model = model, rm = rm, obj = obj)

Após criar a carteira de investimentos, você terá uma alocação recomendada de ativos que visa otimizar os objetivos financeiros estabelecidos. Essa carteira pode então ser usada para tomada de decisões de investimento e para monitoramento contínuo do desempenho.

Rebalancear a Carteira

Após a criação da carteira otimizada, é essencial realizar o rebalanceamento periódico para garantir que a alocação dos ativos continue alinhada com as metas e estratégias definidas. O rebalanceamento ajuda a manter o portfólio em conformidade com os objetivos de investimento, ajustando as proporções dos ativos conforme necessário.

Porém, antes de iniciar o processo de rebalanceamento, é útil selecionar os principais tickers da carteira. Isso permitirá que você se concentre nos ativos mais relevantes e tome decisões informadas sobre ajustes na alocação.

# número desejado de ativos na carteira
n = 5

# Selecionando os principais tickers
top_5_tickers = carteira.sort_values(by='weights', ascending=False).head(n)

# exibe os tickers selecionados
print(top_5_tickers)

Criando um DataFrame de Variação com os Principais Tickers Selecionados

Esta etapa é crucial para calcular a variação dos preços dos principais ativos selecionados ao longo do tempo. Com um DataFrame que contém os dados de variação, você pode analisar como cada ativo se comporta em relação ao seu desempenho passado e ajustar suas estratégias de investimento conforme necessário.

# Criando o DataFrame de variação com os cinco principais tickers
variacao_df_top_5_tickers = variacao_df[top_5_tickers.index.tolist()]

# exibe o DataFrame criado
print(variacao_df_top_5_tickers)

Atualizando Instância da Classe Portfólio

Agora, atualizar a instância da classe Portfólio é uma etapa fundamental para recalcular os parâmetros estatísticos dos ativos com base nos dados mais recentes dos principais tickers selecionados. Esse processo garante que a análise esteja alinhada com as informações mais atualizadas e que a otimização da carteira reflita as mudanças recentes no mercado.

# Atualizando a instância de Portfolio com os dados dos cinco principais tickers
portfolio = rp.Portfolio(returns = variacao_df_top_5_tickers)

Recalculando o Método de Otimização

Com a atualização dos dados e a instância da classe Portfólio, estamos prontos para recalcular a alocação otimizada dos ativos. Esse processo garantirá que nossa carteira de investimentos seja ajustada de acordo com as novas informações e que a alocação dos ativos maximize o retorno esperado enquanto minimiza o risco.

# Recalculando o método de otimização com os dados atualizados
portfolio.assets_stats(method_mu = metodo_mu, method_cov = metodo_cov)

Atualizando a Carteira de Investimentos

Após recalcular a alocação otimizada dos ativos, o próximo passo é atualizar a carteira de investimentos com os novos pesos (weights) calculados. Isso ajusta a distribuição dos ativos na carteira de acordo com a otimização mais recente, garantindo que a estratégia de investimento esteja alinhada com os objetivos definidos e as condições atuais do mercado.

# Atualizando a carteira de investimentos com os novos pesos calculados
carteira = portfolio.optimization(model = model, rm = rm, obj = obj)

Manter a carteira de investimentos atualizada com os novos pesos calculados é crucial para garantir que a alocação dos ativos permaneça eficiente e eficaz. Isso ajuda a otimizar o desempenho da carteira e a alcançar os objetivos financeiros estabelecidos, enquanto responde às mudanças nas condições do mercado e nos dados dos ativos.

Cálculo da Eficiência da Fronteira

Com a carteira rebalanceada e atualizada com os novos pesos, o próximo passo é calcular a eficiência da fronteira. A eficiência da fronteira (ou Fronteira Eficiente) é uma ferramenta crucial na teoria moderna de portfólio, pois nos permite avaliar o desempenho da carteira em termos de retorno esperado e risco, identificando a combinação ótima de ativos que proporciona o melhor retorno para um dado nível de risco.

# Número de pontos da fronteira
pontos = 50

# Calculando a eficiência da fronteira com a carteira rebalanceada
fronteira = portfolio.efficient_frontier(model=model, rm=rm, points=pontos)

# Exibe o resultado para cada ticker
print(fronteira.T.head())

A eficiência da fronteira fornece uma visão clara sobre a performance da carteira, permitindo avaliar se a alocação atual está otimizada e se a carteira está posicionada de forma eficiente em termos de retorno e risco. Isso é essencial para tomar decisões informadas sobre ajustes adicionais na estratégia de investimento e para garantir que a carteira esteja alinhada com seus objetivos financeiros e perfil de risco. 

Resultados

A visualização e a discussão dos resultados são cruciais para compreender e comunicar de forma eficaz as descobertas da nossa análise de portfólio. A seguir, apresentaremos gráficos que ajudarão a ilustrar a composição da nossa carteira de investimentos e os insights obtidos.

Composição da Carteira de Investimentos

Para iniciar, vamos visualizar a composição atual da nossa carteira de investimentos. Este gráfico permitirá identificar a alocação de ativos em nossa carteira e entender como os diferentes ativos contribuem para o perfil geral de risco e retorno.

# Plotando a composição da carteira de investimentos
plot_composicao_carteira = rp.plot_pie(
    w      = carteira,
    title  = 'Composição da Carteira de Investimento',
    others = 0.01,
    nrow   = 25,
    cmap   = "tab20",
    height = 6,
    width  = 10,
    ax     = None
)

Observe o resultado obtido para composição da nossa carteira até agora.

Este gráfico inicial fornece uma visão clara sobre a distribuição dos ativos na carteira e serve como base para discussões mais detalhadas sobre o desempenho e a estratégia de alocação de investimentos.

Eficiência da Fronteira

Para compreender melhor o trade-off entre risco e retorno da nossa carteira otimizada, vamos visualizar a eficiência da fronteira. Esse conceito nos ajuda a identificar as melhores combinações possíveis de risco e retorno, fornecendo uma visão clara sobre como nossa carteira se posiciona em relação às fronteiras de eficiência do mercado.

# ponto_rebalanceamento  = 'Ponto de risco máximo da fronteira'
retorno_esperado = portfolio.mu
covariancia_matrix = portfolio.cov
retornos = portfolio.returns

# Plotando a eficiência da fronteira
plot_eficiencia_fronteira = rp.plot_frontier(
    w_frontier=fronteira,
    mu=retorno_esperado,
    cov=covariancia_matrix,
    returns=retornos, rm=rm,
    alpha=0.05,
    cmap='viridis',
    w=carteira,
    label=ponto_rebalanceamento,
    marker='x', s=16, c='r', height=6, width=10, ax=None)

# Adicionando título
plt.title("Média da fronteira-eficiente - Desvio Padrão (MV)")

# Ajustando o layout para evitar sobreposições
plt.tight_layout()

# Mostrando o gráfico
plt.show()

Onde obtemos o seguinte gráfico.

A linha curva formada pelos pontos é a Fronteira Eficiente, e cada ponto nela representa um portfólio que, para um dado nível de risco, maximiza o retorno esperado. O "Ponto de risco máximo da fronteira" está destacado com um 'X' vermelho e indica o portfólio de maior risco na Fronteira Eficiente, além do qual o aumento de risco não é compensado por um aumento proporcional no retorno esperado.

Medidas de Risco

Medir o risco é essencial para entender a volatilidade e os possíveis prejuízos associados a um portfólio. Cada medida de risco possui características únicas e é adequada para diferentes contextos de investimento. A escolha da medida apropriada depende do perfil do investidor, dos objetivos de investimento e do contexto específico.

Relembrando Algumas Medidas de Risco Utilizadas

A seguir, apresentamos novamente um resumo das principais medidas de risco que serão analisadas:

• MV (Variância): Mede a dispersão dos retornos em relação à média.
• MAD (Desvio Absoluto Médio): Avalia a volatilidade ao calcular a média das diferenças absolutas dos retornos em relação à média.
• MSV (Desvio Padrão Mínimo Variância): Determina o portfólio com o menor desvio padrão para uma dada média de retorno.
• FLPM (Percentual de Perda de Risco): Mede a perda percentual em relação ao valor inicial.
• SLPM (Percentual de Perda de Risco Simples): Calcula a perda percentual simples dos ativos.
• CVaR (Valor em Risco Condicional): Avalia a média das perdas que excedem o Value at Risk (VaR) em um dado nível de confiança.
• EVaR (Valor Esperado em Risco): Mede o valor esperado das perdas além do VaR.
• WR (Risco de Negociação): Avalia o impacto do volume de negociações no risco.
• MDD (Drawdown Máximo): Determina a maior perda acumulada desde o último pico.
• ADD (Drawdown Médio): Avalia a perda média acumulada durante os períodos de drawdown.
• CDaR (Conditional Drawdown at Risk): Mede a perda esperada durante os piores drawdowns.
• UCI (Índice de Custo de Atualização): Avalia o custo associado à atualização do portfólio.
• EDaR (Drawdown Expectation Risk): Calcula a expectativa de drawdown para o portfólio.

Calculando e Visualizando Medidas de Risco

Vamos calcular as medidas de risco para cada uma das estratégias de otimização do portfólio e, em seguida, visualizar esses dados para facilitar a análise.

# Calculando medidas de risco
medidas_risco = ['MV', 'MAD', 'MSV', 'FLPM', 'SLPM', 'CVaR',
                 'EVaR', 'WR', 'MDD', 'ADD', 'CDaR', 'UCI', 'EDaR']

# Realiza o cálculo de risco para cada medidor
carteira_multipla = pd.DataFrame([])
for medidas in medidas_risco:
    carteira_cache = portfolio.optimization(model=model, rm=medidas, obj=obj)
    carteira_multipla = pd.concat([carteira_multipla, carteira_cache], axis=1)
carteira_multipla.columns = medidas_risco

Onde, obtemos graficamente,

# Visualizando medidas de risco
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import LinearSegmentedColormap

# Definindo o mapa de cores personalizado
colors = [(0, 'green'), (0.2, 'gold'), (1, 'red')]
cmap = LinearSegmentedColormap.from_list('CustomMap', colors)

# Plotando heatmap das medidas de risco da carteira com os valores nas células
plt.figure(figsize=(10, 6))
heatmap = plt.imshow(carteira_multipla, cmap=cmap, aspect='auto')
plt.colorbar(label='Medida de Risco')
plt.title('Medidas de Risco da Carteira')
plt.xlabel('Medidas de Risco')
plt.ylabel('Tickers')
plt.xticks(ticks=range(len(medidas_risco)), labels=medidas_risco, rotation=45)
plt.yticks(ticks=range(len(carteira_multipla.index)), labels=carteira_multipla.index)

# Adicionando os valores nas células
for i in range(len(carteira_multipla.index)):
    for j in range(len(medidas_risco)):
        plt.text(j, i, f'{carteira_multipla.iloc[i, j]:.2f}', ha='center', va='center', color='white')

plt.tight_layout()
plt.show()

De forma geral, observamos que o ativo BBSE3.SA apresenta valores de risco mais elevados, especialmente nas métricas FLPM, SLPM, WR e EDaR, refletindo uma maior exposição a perdas significativas e a volatilidade. Em contraste, PRIO3.SA mostra os valores de risco mais baixos em várias métricas, sugerindo uma menor volatilidade e, portanto, um perfil de risco mais conservador.

Backtesting

O backtesting é uma etapa crucial na análise de portfólio, permitindo avaliar o desempenho da nossa estratégia de investimento com base em dados históricos. Esta análise ajuda a entender como a carteira teria se comportado no passado e fornece insights valiosos para otimizar as estratégias de investimento.

Normalizando os Dados

Antes de iniciar o backtesting, é essencial normalizar os dados. A normalização garante que possamos comparar o desempenho da carteira ao longo do tempo de maneira adequada e justa. Este processo envolve ajustar os retornos da carteira em relação ao seu valor inicial, permitindo uma comparação uniforme ao longo do período analisado.

Vamos normalizar os dados históricos para que o desempenho da carteira seja expresso como uma série temporal de retornos relativos ao valor inicial.

# Lista as informações necessárias
dados_tickers_adj = dados_tickers['Adj Close'][top_5_tickers.index.tolist()]

# Normaliza os valores
df_normalizado = dados_tickers_adj/dados_tickers_adj.iloc[0,:]

# Remove linhas sem informação útil
#df_normalizado = df_normalizado.dropna()

# Exibe os dados normalizados
print(df_normalizado)

Comprando os Ativos

Vamos simular a compra dos ativos da nossa carteira de investimentos com base nos pesos atribuídos a cada um. Esta simulação nos ajudará a entender como nosso investimento inicial é alocado entre os diferentes ativos e a projetar o valor da carteira ao longo do tempo.

aporte = 1_000  # Definição do valor do aporte inicial para compra dos ativos

weights = top_5_tickers / np.sum(top_5_tickers)  # Cálculo dos pesos relativos de cada ativo na carteira

# Derreter o DataFrame para torná-lo mais longo (long format), facilitando a visualização dos pesos de cada ativo
pe = top_5_tickers.melt(value_vars=['weights'], var_name='Ação', value_name='Peso')

# Multiplicação dos retornos diários dos ativos pelos pesos de cada ativo na carteira para aplicar a alocação da carteira aos retornos diários
df_normalizado = df_normalizado * carteira.T.values

# Aplicação do aporte inicial na carteira de ativos, multiplicando os retornos normalizados pela carteira pelo valor do aporte
df_normalizado = df_normalizado * aporte

Métricas Importantes

Para avaliar o desempenho da nossa carteira de investimentos, é fundamental calcular e analisar algumas métricas de desempenho. Essas métricas ajudam a entender como a carteira se comportou ao longo do período de backtesting, proporcionando uma visão clara sobre o retorno e o risco.

Primeiro, somamos os valores de todos os ativos na carteira para obter o valor total alocado em cada dia. Esta métrica nos dá uma visão geral do valor investido ao longo do tempo.

Em seguida, calculamos o retorno diário percentual da carteira. Este cálculo é feito dividindo o valor total alocado em cada dia pelo valor total alocado no dia anterior, subtraindo 1 e multiplicando por 100 para obter a porcentagem. Essa métrica mostra a variação diária do valor da carteira.

Após calcular as métricas, removemos quaisquer linhas que contenham valores ausentes (NaN) no DataFrame. Isso é importante para garantir a integridade dos dados e evitar erros em análises subsequentes. E, finalmente, exibimos o DataFrame após as operações realizadas para revisar os resultados e verificar as métricas calculadas.

# Cálculo do valor total alocado em cada dia somando os valores de todos os ativos na carteira
df_normalizado['Valor_Alocado_Dia_R$'] = df_normalizado.sum(axis=1)

# Cálculo do retorno diário percentual da carteira, dividindo o valor total alocado em cada dia pelo valor total alocado no dia anterior e subtraindo 1, multiplicando por 100 para obter a porcentagem
df_normalizado['Retorno_Diario_%'] = ((df_normalizado['Valor_Alocado_Dia_R$'] / df_normalizado['Valor_Alocado_Dia_R$'].shift(1)) -1).fillna(0) * 100

# Remoção de linhas que contenham valores ausentes (NaN) na DataFrame
df_normalizado = df_normalizado.dropna()

# Retorno do DataFrame após as operações realizadas
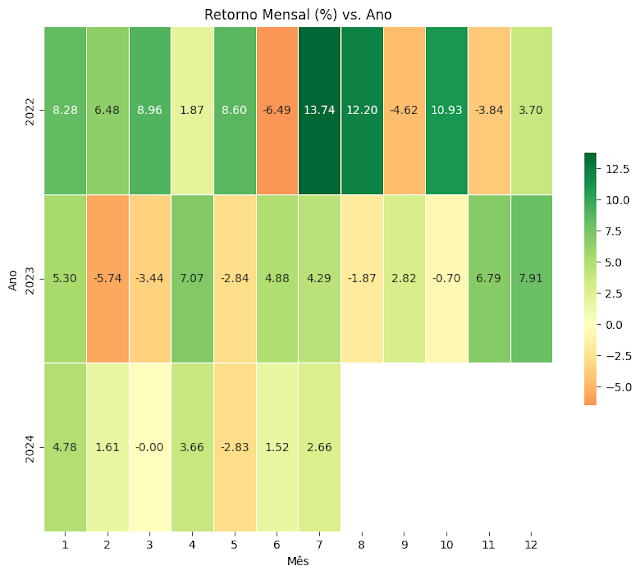
print(df_normalizado)

Desempenho Mensal da Carteira

Para obter uma visão mais clara do desempenho da carteira ao longo do tempo, analisamos o desempenho médio mensal. Esse tipo de análise é crucial para identificar tendências e padrões de performance ao longo dos meses. Vamos criar um gráfico que mostra o desempenho médio da carteira em cada mês do período selecionado.

import seaborn as sns
import matplotlib.pyplot as plt

# Criar uma cópia do DataFrame para manter os dados originais intactos
df_monthly_return = df_normalizado.copy()

# Extrair o ano e o mês da data e criar colunas separadas para eles
df_monthly_return['Year'] = df_monthly_return.index.year
df_monthly_return['Month'] = df_monthly_return.index.month

# Agrupar os retornos mensais por ano e mês e calcular a média
#df_monthly_return = df_monthly_return.groupby(['Year', 'Month']).mean()['Retorno_Diario_%'].unstack()
#df_monthly_return = (df_monthly_return.groupby(['Year', 'Month']).mean()['Valor_Alocado_Dia_R$'].unstack() - aporte ) / aporte * 100
df_monthly_return = df_monthly_return.groupby(['Year', 'Month']).sum()['Retorno_Diario_%'].unstack()

# Mapear os valores positivos para verde e os valores negativos para vermelho
cmap = sns.color_palette("RdYlGn", as_cmap=True)

# Plotar o mapa de calor
plt.figure(figsize=(10, 8))
sns.heatmap(df_monthly_return, annot=True, fmt=".2f", cmap=cmap, center=0, linewidths=.5, cbar_kws={"shrink": 0.5})
plt.title('Retorno Mensal (%) vs. Ano')
plt.xlabel('Mês')
plt.ylabel('Ano')
plt.show()

Visualizando o Desempenho ao Longo do Tempo

Para obter uma visão abrangente do desempenho da nossa carteira de investimentos, é essencial visualizar os resultados do backtesting ao longo do tempo. Esse processo nos ajuda a avaliar a evolução do valor da carteira, o retorno acumulado e outras métricas importantes.

# Importa pyplot
import matplotlib.pyplot as plt

# Plotando o desempenho dos tickers e o valor alocado da carteira ao longo do tempo
plt.figure(figsize=(10, 6))

# Plotando o desempenho dos tickers
for ticker in df_normalizado.columns[:-2]:  # Excluindo as duas últimas colunas (Valor_Alocado_Dia_R$ e Retorno_Diario_%)
    plt.plot(df_normalizado.index, df_normalizado[ticker], label=ticker)

# Plotando o valor alocado da carteira
plt.plot(df_normalizado.index, df_normalizado['Valor_Alocado_Dia_R$'], marker='o', linestyle='-', color='green', label='Carteira')

# Adicionando título e rótulos aos eixos
plt.title('Desempenho dos Tickers e Valor Alocado da Carteira')
plt.xlabel('Período')
plt.ylabel('Desempenho da Carteira')
plt.xticks(rotation=45)
plt.grid(True)
plt.legend()
plt.tight_layout()

# Exibindo o gráfico
plt.show()

Observe na imagem acima, que mostra o gráfico de desempenho dos tickers individuais (ativos) e do valor alocado na carteira ao longo do tempo, de 2022 até o meio de 2024. Cada linha colorida representa o desempenho de um ativo específico, enquanto a linha verde mais espessa representa o desempenho consolidado da carteira. Onde,

• BBSE3.SA (linha azul): Demonstrou um crescimento consistente ao longo do período, apesar de alguma volatilidade.
• PETR4.SA (linha laranja): Apresenta uma trajetória de crescimento mais modesta com flutuações moderadas.
• CIEL3.SA (linha verde): Crescimento relativamente estável, com poucos picos de volatilidade.
• SBSP3.SA (linha vermelha): Mostra o crescimento mais lento e mais estável entre os ativos, com poucas variações abruptas.
• PRIO3.SA (linha roxa): Teve um desempenho mais contido e estável, similar a SBSP3.SA.
• Desempenho da Carteira:

Linha verde escura: A linha grossa representa a performance geral da carteira. Observa-se que a carteira, como um todo, teve um crescimento substancial e contínuo ao longo do período. A trajetória ascendente indica uma valorização significativa, com momentos de alta volatilidade, mas sem quedas abruptas ou prolongadas.

Note ainda que a carteira demonstrou uma boa relação entre risco e retorno, visto que a linha verde escura (carteira) superou consistentemente o desempenho dos ativos individuais. Isso sugere uma diversificação eficaz que dilui o risco individual dos ativos, isto é, a carteira consegue mitigar as quedas de alguns ativos com a alta de outros, resultando em um crescimento mais uniforme e previsível.

Além disso, embora a carteira apresente momentos de volatilidade, estes são amortecidos pela composição diversificada dos ativos. Isto é evidenciado pelo fato de que, mesmo em períodos de variação nos ativos individuais, a linha da carteira não apresenta variações bruscas.

Considerando ainda que a valorização da carteira é expressiva, superando a soma do desempenho dos ativos individuais, indica uma gestão eficiente e a possível aplicação de estratégias de rebalanceamento ou de alocação otimizada de ativos.

Em resumo, a carteira demonstra um desempenho robusto, com boa diversificação e uma relação risco-retorno favorável. Este comportamento sugere uma abordagem prudente e estratégica na alocação de ativos, potencialmente comparável a indicadores de referência de mercado. Para uma análise mais detalhada, seria necessário comparar diretamente com benchmarks como o Ibovespa ou índices de referência internacionais, além de avaliar métricas como Sharpe Ratio, Beta e outros indicadores de performance ajustada ao risco.

Calculando o ROI da Carteira

ganho_obtido = df_normalizado['Valor_Alocado_Dia_R$'][-1]
valor_investido = aporte
ROI = ((ganho_obtido - valor_investido)/valor_investido)*100
print('O ROI da Carteira é de',round(ROI),'%.')
print('O investimento inicial de',
      round(valor_investido),'corresponde agora ao valor de',
      round(ganho_obtido),'isto é, uma diferença de', round(ganho_obtido-valor_investido))

Para nossa carteira selecionada, tem-se um ROI estimado em 149 %.

Comparando o Desempenho da Carteira com Benchmark

Para uma análise completa, é fundamental comparar o desempenho da sua carteira com benchmarks relevantes como o Ibovespa, o CDI e o IPCA. Esses índices e taxas fornecem uma base de comparação para avaliar se a carteira está superando, igualando ou ficando aquém dos principais indicadores de mercado.

# Importar dados do Ibovespa
ibov = yf.download("^BVSP", start=data_inicial, end=data_final)["Adj Close"]

# Importar dados do CDI do URL fornecido
url_cdi = "https://api.bcb.gov.br/dados/serie/bcdata.sgs.11/dados?formato=json&dataInicial={}&dataFinal={}".format(data_inicial.strftime('%d/%m/%Y'), data_final.strftime('%d/%m/%Y'))
dados_cdi = pd.read_json(url_cdi)
dados_cdi['data'] = pd.to_datetime(dados_cdi['data'], dayfirst=True)
dados_cdi.set_index('data', inplace=True)

# Normalizar os dados do Ibovespa entre si
ibov_normalized = ibov / ibov.iloc[0] - 1

# Normalizar os dados da sua carteira
carteira_normalized = df_normalizado.sum(axis=1) / df_normalizado.sum(axis=1).iloc[0] - 1

# Calcular o crescimento percentual diário do CDI
cdi_daily_growth = dados_cdi['valor'] / 100 + 1

# Normalizar os dados do CDI, convertendo para a escala correta
# cdi_normalized = ((dados_cdi['valor'] / dados_cdi['valor'].iloc[0]) / 100) + 1
# Normalizar os dados do CDI
cdi_normalized = cdi_daily_growth.cumprod() -1

# Importar dados do IPCA do URL fornecido
url_ipca = "https://api.bcb.gov.br/dados/serie/bcdata.sgs.433/dados?formato=json&dataInicial={}&dataFinal={}".format(data_inicial.strftime('%d/%m/%Y'), data_final.strftime('%d/%m/%Y'))
dados_ipca = pd.read_json(url_ipca)
dados_ipca['data'] = pd.to_datetime(dados_ipca['data'], dayfirst=True)
dados_ipca.set_index('data', inplace=True)

# Calcular o crescimento percentual diário do IPCA
ipca_daily_growth = dados_ipca['valor'] / 100 + 1

# Normalizar os dados do IPCA
ipca_normalized = ipca_daily_growth.cumprod() - 1

# Fundir os dados da carteira e do IPCA usando as datas como chave de junção
#carteira_ipca = pd.merge(carteira_normalized.to_frame(), ipca_normalized, left_index=True, right_index=True, how='inner')

# Calcular a diferença entre o desempenho da carteira e o IPCA
#diferenca_carteira_ipca = carteira_ipca[0] - carteira_ipca['valor']

# Importar dados do preço do Bitcoin
bitcoin = yf.download("BTC-USD", start=data_inicial, end=data_final)["Adj Close"]

# Normalizar os dados do Bitcoin entre si
bitcoin_normalized = bitcoin / bitcoin.iloc[0] - 1

# Plotar os retornos acumulados normalizados no mesmo gráfico
plt.figure(figsize=(12, 6))
plt.plot(ibov_normalized.index,     100*ibov_normalized, label='Ibovespa', color='blue', linewidth=0.5)
plt.plot(cdi_normalized.index,      100*cdi_normalized, label='CDI', color='red', linewidth=0.5)
plt.plot(ipca_normalized.index,     100*ipca_normalized, label='IPCA', color='orange', linewidth=0.5)
#plt.plot(diferenca_carteira_ipca.index, 100*diferenca_carteira_ipca, label='Diferença de Carteira - IPCA', color='purple')
plt.plot(bitcoin_normalized.index,  100*bitcoin_normalized, label='Bitcoin', color='purple', linewidth=0.5)  # Adicionando Bitcoin
plt.plot(carteira_normalized.index, 100*carteira_normalized, label='Minha Carteira', color='green')
plt.xlabel('Período')
plt.ylabel('Retorno Acumulado Normalizado (%)')
plt.title('Desempenho da Carteira vs. Ibovespa vs. CDI vs. IPCA vs BTC')
plt.legend()
plt.grid(True, which='both', alpha=0.5, linewidth=0.5)
plt.show()

O desempenho da nossa carteira de investimentos na B3, ao longo do tempo, tem se destacado de forma notável quando comparado a diversos benchmarks de mercado, como o Ibovespa, o CDI, o IPCA e o Bitcoin, por exemplo. 

Observando o gráfico de desempenho, é evidente que, enquanto o Ibovespa apresenta uma trajetória estável com crescimento leve ao longo do período, sua volatilidade significativa destaca a natureza intrínseca dos ativos de renda variável. Em contraste, o CDI, como um indicador de renda fixa, exibe um crescimento constante e previsível, mas seus retornos são modestos quando comparados ao desempenho da nossa carteira. 

O IPCA, por sua vez, refletindo a inflação acumulada, mostra um crescimento estável que foi superado de maneira substancial pela nossa carteira, indicando que conseguimos não apenas manter, mas aumentar nosso poder de compra ao longo do tempo.  Já, o Bitcoin ilustra a alta volatilidade típica das criptomoedas, com picos e quedas acentuados. Embora tenha experimentado momentos de crescimento explosivo, a consistência de retornos da nossa carteira destaca uma gestão de investimentos mais equilibrada e eficiente no período considerado. 

Nossa carteira, de forma geral, mostra um crescimento consistente e significativo. Esse desempenho robusto sugere uma seleção de ativos bem-sucedida e uma estratégia de gerenciamento de riscos que tem sido eficaz em capturar oportunidades de mercado, dentro do escopo considerado para gestão de risco de nossa carteira. Manter a diversificação e fazer ajustes táticos conforme necessário serão cruciais para continuar aproveitando o crescimento observado. A análise semanal e sazonal pode ser particularmente útil para otimizar retornos e mitigar riscos, garantindo que nossa carteira continue a superar as expectativas.

Aplicando o Prophet

Agora, também é possível observar que a previsão de preços utilizando o modelo Prophet oferece uma visão otimista para os próximos 180 dias. 

import yfinance as yf
from prophet import Prophet
import matplotlib.pyplot as plt
import pandas as pd

# Função para obter os dados históricos de um ativo da B3
def obter_dados_ativo(ticker, data_inicial, data_final):
    # Obtendo os dados históricos do ativo
    dados = yf.download(ticker, start=data_inicial, end=data_final)
    return dados

# Função para fazer a previsão de preço usando o Prophet
def fazer_previsao(dados):
    # Renomeando as colunas para o formato esperado pelo Prophet
    dados = dados.reset_index()
    dados = dados.rename(columns={'Date': 'ds', 'Adj Close': 'y'})

    # Criando uma instância do Prophet e ajustando aos dados
    modelo = Prophet()
    modelo.fit(dados)

    # Criando datas futuras para a previsão
    futuro = modelo.make_future_dataframe(periods = 180)  # Previsão para os próximos 90 dias

    # Fazendo a previsão
    previsao = modelo.predict(futuro)
    return modelo, previsao

# Função para plotar vários gráficos da previsão de preço
def plotar_graficos_previsao(modelo, previsao):
    # Plotando o gráfico da previsão de preço
    figura = modelo.plot(previsao, xlabel='Data', ylabel='Preço', figsize=(10, 6))
    plt.title('Previsão de Preço e Intervalo de Confiança')
    plt.xlabel('Período')
    plt.ylabel('Valor Alocado')
    plt.show()

    # Plotando os componentes do modelo
    figura = modelo.plot_components(previsao, figsize=(10, 6))
    plt.xlabel('Período Considerado')
    plt.ylabel('Variação')
    plt.show()

# Suponha que df_normalizado seja seu DataFrame contendo os dados normalizados da carteira
# Normalizar os dados da sua carteira
carteira_normalized = df_normalizado.sum(axis=1) / df_normalizado.sum(axis=1).iloc[0] - 1

# Fazendo a previsão de preço da carteira usando Prophet
modelo_carteira, previsao_carteira = fazer_previsao(carteira_normalized.to_frame().reset_index().rename(columns={'index': 'ds', 0: 'y'}))

# Plotando vários gráficos da previsão de preço
plotar_graficos_previsao(modelo_carteira, previsao_carteira)

Os dados históricos indicam um crescimento contínuo e a projeção mantém essa tendência positiva. A linha azul escura no gráfico abaixo de previsão sugere uma valorização contínua, apesar do aumento da incerteza ao longo do tempo, representado pela área sombreada em azul claro.

Por sua vez, analisando os componentes da previsão, a tendência geral aponta para um crescimento consistente, reforçando a expectativa de continuidade no bom desempenho da nossa carteira. 

Conclusão

A aplicação da Teoria Moderna de Portfólio (MPT) de Markowitz, utilizando Python e dados da Bolsa de Valores Brasileira (B3), revela-se uma abordagem eficaz e robusta para a otimização de carteiras de investimentos. A combinação de métodos quantitativos com a capacidade computacional do Python permite a análise de grandes volumes de dados de forma precisa e detalhada, facilitando a identificação de portfólios eficientes e otimizados.

Os resultados deste estudo destacam a importância da diversificação, conforme estabelecido por Markowitz, como uma estratégia essencial para mitigar riscos e maximizar retornos ajustados ao risco. A utilização de bibliotecas Python como Pandas e NumPy, junto a ferramentas de visualização como Matplotlib, não apenas simplifica a implementação prática dos conceitos teóricos, mas também torna essas técnicas acessíveis a analistas e investidores, promovendo uma análise mais informada e detalhada.

O emprego de dados reais da B3 agrega uma dimensão prática relevante, demonstrando que os princípios de Markowitz são plenamente aplicáveis ao contexto do mercado financeiro brasileiro. A flexibilidade do framework permite ajustar parâmetros e simular cenários econômicos diversos, o que reforça a utilidade dessa abordagem na formulação de estratégias de investimento sofisticadas e adaptativas.

Assim, a integração da teoria de Markowitz com ferramentas modernas de programação proporciona uma poderosa ferramenta para a gestão de portfólios, permitindo decisões de investimento mais embasadas e precisas. Este estudo reafirma a relevância contínua da teoria de portfólio na prática contemporânea e sugere que o avanço tecnológico e o acesso crescente a dados financeiros detalhados ampliam significativamente as possibilidades de inovação na gestão de investimentos.

Para pesquisas futuras, recomenda-se a exploração de técnicas complementares, como a otimização por fronteira de Pareto e a incorporação de algoritmos de machine learning. Essas abordagens têm o potencial de aumentar ainda mais a precisão das previsões e a eficiência das alocações de ativos, abrindo novas fronteiras na interseção entre finanças, economia e tecnologia. A contínua evolução nesse campo promete transformar a maneira como entendemos e aplicamos estratégias de investimento, proporcionando insights mais profundos e soluções mais eficazes para os desafios da gestão de portfólios.

Referências

[1] Markowitz, Harry. "Portfolio Selection." The Journal of Finance, 1952. 

[2] Elton, Edwin J., and Martin J. Gruber. "Modern Portfolio Theory, 1950 to Date." Journal of Banking & Finance, 1997. 

[3] Nobel Prize. "The Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel 1990." 

[4] Statman, Meir. "How Many Stocks Make a Diversified Portfolio?" Journal of Financial and Quantitative Analysis, 1987.

[5] Malkiel, Burton G. "A Random Walk Down Wall Street." W.W. Norton & Company, 2003. 

[6] B3 - Brasil, Bolsa, Balcão. "Institutional Information."